

Pierre CRESPIN |
Etude sur le quinzième pavage pentagonal du plan |
Réponses en Images |
Réponses en images (pour l'essentiel)
Cliquez sur les images pour obtenir des figures présentant tous les angles liés au pavé Penta15. |
||
 |
||
 |
||
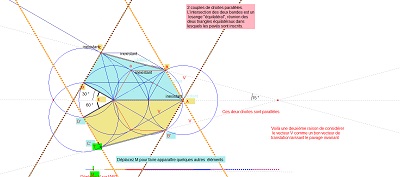
| Ci-dessous: "Du pavé ... au bloc de trois pavés", avec des symétries axiales et quelques propriétés à chaque étape, et enfin, un essai d'assemblage de blocs. | Autres éléments liés aux paires de pavés symétriques |
 |
|
Ci-dessous et ci-contre : Découverte des translations potentielles et vérification sur un assemblage |
 |
 |
|
 |
 |
.jpg) |
 |
 |
|
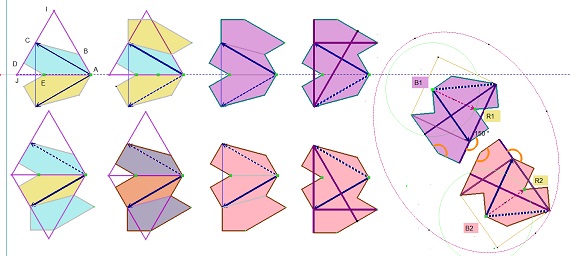
Et ci-dessous : variation sur le thème des bonnes propriétés de ces blocs (ces blocs sont très riches, ce qui les rend très particuliers) |
|
 |
|
Voir leurs propriétés illustrées par une figure Cabri , en particulier à nouveau les angles de pi/12 (mais cette fois pour tous ou presque) . Sortir les points M0 à M6 dans la figure Cabri ci-contre. |
 |
Les deux types de blocs de 3 pavés Penta15 sont désormais les tuiles que nous voulons assembler. Il est possible que cela n'aboutisse pas, mais si on y parvient, on aura ainsi obtenu, aussi, un pavage par Penta15 en remplissant ces blocs par les trois pavés contenus. Assemblages des blocs de ces deux types |
|
Aller plus vite vers la conclusion ? cliquer ici |
|
Vous découvrirez que les assemblages valides de ces blocs de trois pavés sont en fait réduits à trois (une translation, une ou deux symétries centrales et un ou deux assemblages par les deux côtés des angles 150°, moins évident celui-ci ). Lorsqu'il y a un choix entre deux, il importe peu car l'assemblage suivant sera alors fixé. Le résultat sur les deux étapes est globalement le même et donc, il n'y a presque aucune hésitation à avoir. et aussi plus rapidement les images du pavage à partir d'autres blocs. |
|
| vers conclusion |